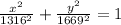Answer:
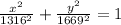
Explanation:
An ellipse is the locus of a point such that its distances from two fixed points, called foci, have a sum that is equal to a positive constant.
The equation of an ellipse with a center at the origin and the x axis as the minor axis is given by:
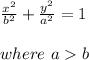
Since the distance of the satellite from the surface of the moon varies from 357 km to 710 km, hence:
b = 357 km + 959 km = 1316 km
a = 710 km + 959 km = 1669 km
Therefore the equation of the ellipse is: