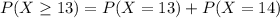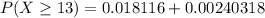Answer:

Explanation:
From the question we are told that:
Probability of curing patients P(x)=0.65
Sample size n=14
Generally the Binomial equation is mathematically given by
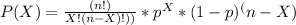
Generally the equation for Equation for at least 12 cured is mathematically given by
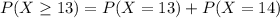
For
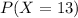
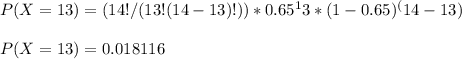
For
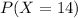
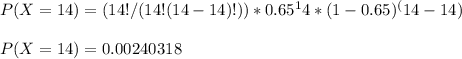
Therefore