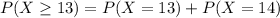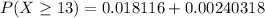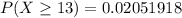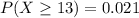Question

A new drug cures 65% of the patients who take it. If it is given to 14 patients, what is the probability that at least 12 will be cured?

Answer 1

`P(X \geq 13) = 0.021`

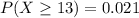
Explanation:

From the question we are told that:

Probability of curing patients P(x)=0.65

Sample size n=14

Generally the Binomial equation is mathematically given by

`P(X) =((n!))/(X!(n-X)!))) *p^X*(1-p)^(n-X)`

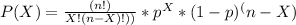
Generally the equation for Equation for at least 12 cured is mathematically given by

`P(X \geq 13) = P(X = 13)+P(X = 14)`

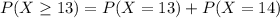
For
`P(X = 13)`

`P(X = 13) = (14!/(13!(14-13)!))*0.65^13*(1-0.65)^(14-13) \\\\P(X = 13)= 0.018116`

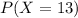
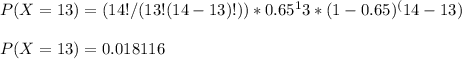
For
`P(X = 14)`

`P(X = 14) = (14!/(14!(14-14)!))*0.65^14*(1-0.65)^(14-14) \\\\P(X = 14)= 0.00240318`

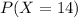
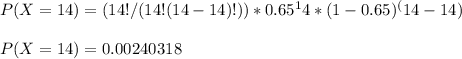
Therefore

`P(X \geq 13) =P(X = 13)+P(X = 14)`

`P(X \geq 13) = 0.018116+0.00240318`

`P(X \geq 13) = 0.02051918`

`P(X \geq 13) = 0.021`