Answer:
The p-value of the test is of 0.0536 > 0.02, which means that there is not sufficient evidence at the 0.02 level to support the executive's claim.
Explanation:
A publisher reports that 75% of their readers own a particular make of car. A marketing executive wants to test the claim that the percentage is actually different from the reported percentage.
At the null hypothesis, we test if the proportion is of 75%, that is:
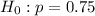
At the alternate hypothesis, we test if the proportion is different of 75%, that is:
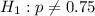
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
75% is tested at the null hypothesis:
This means that
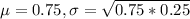
A random sample of 280 found that 70% of the readers owned a particular make of car.
This means that
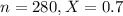
Value of the test statistic:

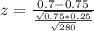
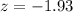
P-value of the test and decision:
The p-value of the test is the probability of finding a sample proportion differing from 0.75 by at least |0.7 - 0.75| = 0.05, which is P(|z| > 1.93), which is 2 multiplied by the p-value of z = -1.93.
Looking at the z-table, z = -1.93 has a p-value of 0.0268.
2*0.0268 = 0.0536.
The p-value of the test is of 0.0536 > 0.02, which means that there is not sufficient evidence at the 0.02 level to support the executive's claim.