Answer:
The maximum amount of red kryptonite present is 33.27 g after 4.93 hours.
Explanation:
dy/dt = y(1/t - k)
separating the variables, we have
dy/y = (1/t - k)dt
dy/y = dt/t - kdt
integrating both sides, we have
∫dy/y = ∫dt/t - ∫kdt
㏑y = ㏑t - kt + C
㏑y - ㏑t = -kt + C
㏑(y/t) = -kt + C
taking exponents of both sides, we have
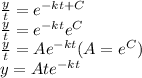
when t = 1 hour, y = 15 grams. So,
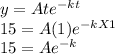 (1)
(1)
when t = 3 hours, y = 30 grams. So,
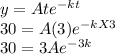 (2)
(2)
dividing (2) by (1), we have
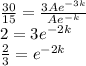
taking natural logarithm of both sides, we have
-2k = ㏑(2/3)
-2k = -0.4055
k = -0.4055/-2
k = 0.203
From (1)
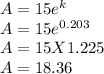
Substituting A and k into y, we have
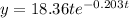
The maximum value of y is obtained when dy/dt = 0
dy/dt = y(1/t - k) = 0
y(1/t - k) = 0
Since y ≠ 0, (1/t - k) = 0.
So, 1/t = k
t = 1/k
So, the maximum value of y is obtained when t = 1/k = 1/0.203 = 4.93 hours

So the maximum amount of red kryptonite present is 33.27 g after 4.93 hours.