Question

A statistician has analysed the duration of audience laughter after a stand up comedian's jokes. The data showed that the laughter duration was evenly distributed between 4 seconds and 9.7 seconds. Then, the probability that the laughter after one of this comedian's jokes lasts for more than 7 seconds is

Answer 1

The probability that the laughter after one of the comedians jokes lasts for more than 7 seconds is approximately 0.474

Explanation:

The nature of the distribution of the given data = Evenly distributed data

The range of the laughter times = Between 4 seconds and 9.7 seconds

The probability density function, f(x), is given as follows;

`f(x) = (1)/(b - a)`

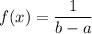
The mean of the uniform distribution, μ, is given as follows;

`\mu = (a + b)/(2)`

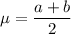
The standard deviation, σ, is given as follows;

`\sigma = \sqrt{(\left (b - a\right)^2)/(12) }`

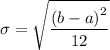
Where;

a = 4, and b = 9.7, we have;

μ = (4 + 9.7)/2 = 6.85

σ = √((9.7 - 4)²/12) ≈ 1.64545

The probability density function, f(x) = 1/(b - a) for a ≤ x ≤ b

∴ f(x) = 1/(9.7 - 4)

For P(x > 7), we have;

P(x > 7) = 1 - P(x < 7) = 1 - (7 - 4) × 1/(9.7 - 4) ≈ 0.474

The probability that the laughter after one of the comedians jokes lasts for more than 7 seconds P(x >7) ≈ 0.474.