Answer:
The probability that the laughter after one of the comedians jokes lasts for more than 7 seconds is approximately 0.474
Explanation:
The nature of the distribution of the given data = Evenly distributed data
The range of the laughter times = Between 4 seconds and 9.7 seconds
The probability density function, f(x), is given as follows;
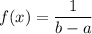
The mean of the uniform distribution, μ, is given as follows;
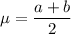
The standard deviation, σ, is given as follows;
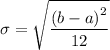
Where;
a = 4, and b = 9.7, we have;
μ = (4 + 9.7)/2 = 6.85
σ = √((9.7 - 4)²/12) ≈ 1.64545
The probability density function, f(x) = 1/(b - a) for a ≤ x ≤ b
∴ f(x) = 1/(9.7 - 4)
For P(x > 7), we have;
P(x > 7) = 1 - P(x < 7) = 1 - (7 - 4) × 1/(9.7 - 4) ≈ 0.474
The probability that the laughter after one of the comedians jokes lasts for more than 7 seconds P(x >7) ≈ 0.474.