Answer:
The options are not given, so I will answer in a general way:
A quadratic equation can be written, in general form, as:
y = a*x^2 + b*x + c
Then if we want this, we need to replace:
a = 1
b = -3
c = -5
Then the equation that we want is:
y = x^2 - 3*x - 5
Is likely that the options are in the factorized way to write a quadratic equation (so it is kinda harder to you)
Such that the factorized way is written as:
y = (x - k)*(x - h)
where k and h are the roots of the quadratic equation.
So you just need to expand that expression and find the one that looks like:
y = x^2 - 3*x - 5
Just to be complete, let's find the factorized form of this particular quadratic equation.
The roots are given by:
0 = x^2 - 3*x - 5
And the two solutions are given by Bhaskara's formula:
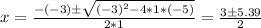
The two roots are:
h = (3 + 5.39)/2 = 4.195
k = (3 - 5.39)/2 = -1.195
Then the factorized form is:
y = (x - 4.195)*(x + 1.195)