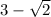Answer:
1
the equation (x-4)^2-17=8 has two solutions because it is in a quadratic form.
(x-4)^2-17=8
x²-8x+16-17-8=0
x²-8x-9=0
Doing middle term factorization
x²-9x+x-9=0
x(x-9)+1(x-9)=0
(x-9)(x+1)=0
either
x=9
x=9or
x=9orx=-1
2.
x^2+4x+3=0:
Doing middle term factorization
x²+3x+x+3=0
x(x+3)+1(x+3)=0
(x+3)(x+1)=0
either
x=-3
or
x=-1
Josh’s solution is incorrect because he missed x=-3.
3.
x^2-6x+7=0
By using quadratic equation formula:
Comparing above equation with ax²+bx+c=0
we get
a=1
b=-6
c=7
Now
we have
x=
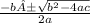
x=

x=
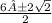
x=

Taking positive
x=

taking negative
x=