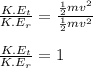Answer:

Step-by-step explanation:
The translational kinetic energy of the hoop is given as:
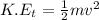 ---------------------- equation (1)
---------------------- equation (1)
where,
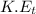 = translational kinetic energy
= translational kinetic energy
m = mass of hoop
v = linear speed of hoop
The rotational kinetic energy of the hoop is given as:

where,
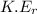 = rotational kinetic energy of the hoop
= rotational kinetic energy of the hoop
I = Moment of Inertia of the hoop = mr²
r = radius of the hoop
ω = angular speed of hoop =
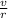
Therefore,
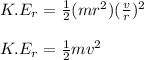 ------------------- equation (2)
------------------- equation (2)
dividing equation (1) and equation (2), we get: