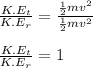Question

g hoop rolls without slipping on a horizontal surface. The hoop has a mass m and radius r. What is the ratio of the hoop's translational kinetic energy to the hoop's rotational kinetic energy, KT /KR

Answer 1

`(K.E_t)/(K.E_r) = 1`

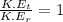
Step-by-step explanation:

The translational kinetic energy of the hoop is given as:

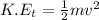`K.E_t = (1)/(2) mv^2` ---------------------- equation (1)

where,

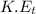`K.E_t` = translational kinetic energy

m = mass of hoop

v = linear speed of hoop

The rotational kinetic energy of the hoop is given as:

`K.E_r = (1)/(2) I\omega^2`

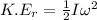
where,

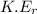`K.E_r` = rotational kinetic energy of the hoop

I = Moment of Inertia of the hoop = mr²

r = radius of the hoop

ω = angular speed of hoop =
`(v)/(r)`

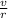
Therefore,

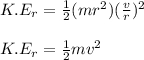`K.E_r = (1)/(2) (mr^2)((v)/(r) )^2\\\\K.E_r = (1)/(2) mv^2`------------------- equation (2)

dividing equation (1) and equation (2), we get:

`(K.E_t)/(K.E_r) = ((1)/(2)mv^2 )/((1)/(2)mv^2 )\\\\(K.E_t)/(K.E_r) = 1`