Question

A section of a parallel-plate air waveguide with a plate separation of 7.11 mm is constructed to be used at 15 GHz as an evanescent wave attenuator to attenuate all the modes except the TEM mode along the guide. Find the minimum length of this attenuator needed to attenuate each mode by at least 100 dB. Assume perfect conductor plates.

Answer 1

the required minimum length of the attenuator is 3.71 cm

Step-by-step explanation:

Given the data in the question;

we know that;

`f_{c_1` = c / 2a

where f is frequency, c is the speed of light in air and a is the plate separation distance.

we know that speed of light c = 3 × 10⁸ m/s = 3 × 10¹⁰ cm/s

plate separation distance a = 7.11 mm = 0.0711 cm

so we substitute

`f_{c_1` = 3 × 10¹⁰ / 2( 0.0711 )

`f_{c_1` = 3 × 10¹⁰ cm/s / 0.1422 cm

`f_{c_1` = 21.1 GHz which is larger than 15 GHz { TEM mode is only propagated along the wavelength }

Now, we determine the minimum wavelength required

Each non propagating mode is attenuated by at least 100 dB at 15 GHz

so

Attenuation constant TE₁ and TM₁ expression is;

∝₁ = 2πf/c × √( (
`f_{c_1` / f)² - 1 )

so we substitute

∝₁ = ((2π × 15)/3 × 10⁸ m/s) × √( (21.1 / 15)² - 1 )

∝₁ = 3.1079 × 10⁻⁷

∝₁ = 310.79 np/m

Now, To find the minimum wavelength, lets consider the design constraint;

20log₁₀
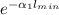`e^{-\alpha _1l_{min` = -100dB

we substitute

20log₁₀
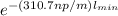`e^{-(310.7np/m)l_{min` = -100dB

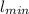`l_{min` = 3.71 cm

Therefore, the required minimum length of the attenuator is 3.71 cm