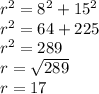Answer:
17 inches
Explanation:
See the attached image. Connect the center of the circle to one endpoint of the chord. That forms a right triangle because the radius is drawn perpendicular to the chord -- that's how the distance from center to chord is measured.
The radius splits the chord into two equal parts, each 15 inches long.
The right triangle has legs 8 and 15, so use the Pythagorean Theorem.