Answer:
B = 49.1°
C = 93.9°
c = 77.9
Explanation:
Given:
a = 47, b = 59, and A = 37°
Required:
B, C, and c
Solution:
✔️To find B, apply the law of sines:
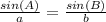
Plug in the values
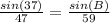
Cross multiply
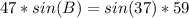
Divide both sides by 47
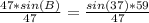
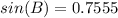
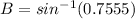
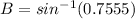
B = 49.0690779° ≈ 49.1° (nearest tenth)
✔️C = 180° - (A + B) (sum of triangle)
C = 180° - (37° + 49.1°)
C = 93.9°
✔️To find c, apply the law of sines:
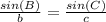
Plug in the values
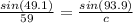
Cross multiply
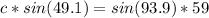
Divide both sides by sin(49.1)
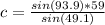
c = 77.8766982
c ≈ 77.9 (nearest tenth)