Need help with inscribed angles If M

Question

asked Nov 26, 2022 56.7k views

1 Answer

Oleg Somov · Answer 1 · 2022-11-30T15:12:12+0000

Given:

In the given circle O, BC is diameter, OA is radius, DC is a chord parallel to chord BA and
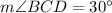$m\angle BCD=30^\circ$ .

To find:

The
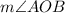$m\angle AOB$ .

Solution:

If a transversal line intersect two parallel lines, then the alternate interior angles are congruent.

We have, DC is parallel to BA and BC is the transversal line.

$\angle OBA\cong \angle BCD$ [Alternate interior angles]

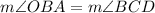
$m\angle OBA=m\angle BCD$

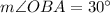
$m\angle OBA=30^\circ$

In triangle AOB, OA and OB are radii of the circle O. It means OA=OB and triangle AOB is an isosceles triangle.

The base angles of an isosceles triangle are congruent. So,

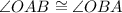$\angle OAB\cong \angle OBA$ [Base angles of an isosceles triangle]

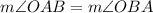
$m\angle OAB=m\angle OBA$

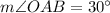
$m\angle OAB=30^\circ$

Using the angle sum property in triangle AOB, we get

$m\angle OAB+m\angle OBA+m\angle AOB=180^\circ$

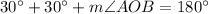
$30^\circ+30^\circ+m\angle AOB=180^\circ$

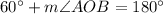
$60^\circ+m\angle AOB=180^\circ$

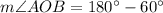
$m\angle AOB=180^\circ-60^\circ$

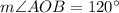
$m\angle AOB=120^\circ$

Hence, the measure of angle AOB is 120 degrees.