Answer:
A
Explanation:
Recall that sin = opposite over hypotenuse
For ∠A we are already given its opposite side length ( 2 ) however the hypotenuse has not been identified.
The triangle shown is a right triangle ( indicated by the little square on the bottom left ) which means that we can find a missing side length, more specifically the hypotenuse, using the Pythagorean theorem
 where a and b = legs and c = hypotenuse
where a and b = legs and c = hypotenuse
we are given that the legs = 2 and 4 and need to find the hypotenuse
That being said we plug in what we are given and solve for c
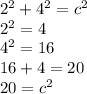
In order to get the exact value of c we must get rid of the exponent.
To do so we can take the square root of both sides
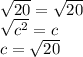
hence, the hypotenuse = √20
Now lets look back at the question
Find sin∠A to the nearest hundredth.
well remember sin = opposite over hypotenuse
The opposite of sin∠A is 2 and the hypotenuse is √20
Hence, sin∠A =
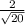 which is equivalent to .447213595
which is equivalent to .447213595
Our last step is to round to the nearest hundredth
We get the sin∠A = .45