Question

Help would be appreciated for this question!!!

Answer 1

A

Explanation:

Recall that sin = opposite over hypotenuse

For ∠A we are already given its opposite side length ( 2 ) however the hypotenuse has not been identified.

The triangle shown is a right triangle ( indicated by the little square on the bottom left ) which means that we can find a missing side length, more specifically the hypotenuse, using the Pythagorean theorem

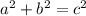`a^2+b^2=c^2` where a and b = legs and c = hypotenuse

we are given that the legs = 2 and 4 and need to find the hypotenuse

That being said we plug in what we are given and solve for c

`2^2+4^2=c^2\\2^2=4\\4^2=16\\16+4=20\\20=c^2`

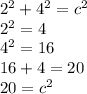
In order to get the exact value of c we must get rid of the exponent.

To do so we can take the square root of both sides

`√(20) =√(20) \\√(c^2) =c\\c=√(20)`

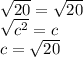
hence, the hypotenuse = √20

Now lets look back at the question

Find sin∠A to the nearest hundredth.

well remember sin = opposite over hypotenuse

The opposite of sin∠A is 2 and the hypotenuse is √20

Hence, sin∠A =
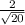`(2)/(√(20) )` which is equivalent to .447213595

Our last step is to round to the nearest hundredth

We get the sin∠A = .45