Answer:
Option A.
Explanation:
Function f:
For x between -1 and 2, the values of f(x) increase, which means that f(x) is increasing.
Function g:
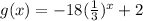
Between -1 and 2:
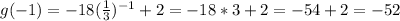
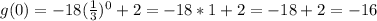

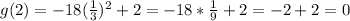
Both are increasing.
However, g starts with a lower value, and finishes with a higher value, which means that function g increases at a faster average rate, and the correct answer is given by option A.