Answer:
The average rate of change of the function over the interval is of 6.
Explanation:
Average rate of change:
The average rate of change of a function h(x) over an interval [a,b] is given by:
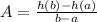
In this question:
Over the interval [-9,-2], so

The function is:
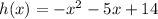
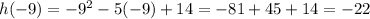
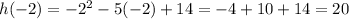
Then
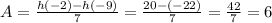
The average rate of change of the function over the interval is of 6.