Answer:
The 95% confidence interval for the true percentage of all adults over 30 who shop at that mall who admit to having lost their car at the mall is (25.37%, 43.93%).
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the z-score that has a p-value of
 .
.
Of 101 randomly selected adults over 30 who frequent a very large mall, 35 admitted to having lost their car at the mall.
This means that
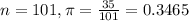
95% confidence level
So
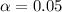 , z is the value of Z that has a p-value of
, z is the value of Z that has a p-value of
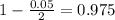 , so
, so
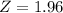 .
.
The lower limit of this interval is:
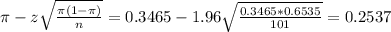
The upper limit of this interval is:

As percentages:
0.2537*100% = 25.37%
0.4393*100% = 43.93%
The 95% confidence interval for the true percentage of all adults over 30 who shop at that mall who admit to having lost their car at the mall is (25.37%, 43.93%).