Answer:
Explanation:
1). From the triangle given in the figure,
m∠BAD = 26°
By applying tangent rule in ΔADB,
tan(∠BAD) =

tan(26°) =
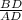
BD = 21[tan(26°)]
BD = 10.24
By applying sine rule in ΔBDC,
sin(52°) =
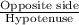
sin(52°) =
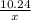
x =
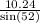
x = 12.99
x ≈ 13.0 units
2). By applying cosine rule in ΔADB,
cos(39°) =
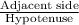
cos(39°) =
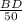
BD = 50cos(39°)
BD = 38.86
By applying sine rule in ΔBDC,
sin(24°) =
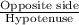
sin(24°) =
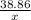
x =
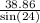
x = 95.54
x ≈ 95.5 units