Answer:
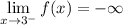
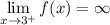
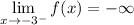
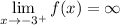
General Formulas and Concepts:
Algebra I
Algebra II
- Analyzing Cartesian Planes and Graphs
Calculus
Limits
- Left Limit:
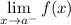
- Right Limit:
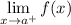
Graphical Limits
Explanation:
We approach this question by analyzing the graph. We notice we have asymptotes at x = -3 and x = 3.
Question 1

Essentially, the question is asking what the value is for f(x) when x approaches 3 from the left. We see from the graph f(x) that if we approach 3 from the left, we would be going towards the x = 3 asymptote, specifically -∞.
∴
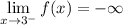
Question 2
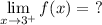
Essentially, the question is asking what the value is for f(x) when x approaches 3 from the right. We see from the graph f(x) that if we approach 3 from the right, we would be going towards the x = 3 asymptote, specifically ∞.
∴
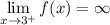
Question 3
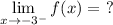
Essentially, the question is asking what the value is for f(x) when x approaches -3 from the left. We see from the graph f(x) that if we approach -3 from the left, we would be going towards the x = -3 asymptote, specifically -∞.
∴
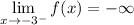
Question 4
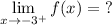
Essentially, the question is asking what the value is for f(x) when x approaches -3 from the right. We see from the graph f(x) that if we approach -3 from the right, we would be going towards the x = -3 asymptote, specifically ∞.
∴
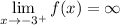
Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Limits
Book: College Calculus 10e