Question

PLEASE HELP!!! On a coordinate plane, a curve approaches x = negative 3, has inflection point (0, 1), and approaches x = 3 in quadrant 1 and 4. A curve approaches x = 3 in quadrant 1, and another curve approaches x = negative 3 in quadrant 3.

Use the graph of f(x) to describe the limits of the function.

Limit of f (x) as x approaches 3 minus=
and Limit of f (x) as x approaches 3 plus=

Limit of f (x) as x approaches negative 3 minus=
and Limit of f (x) as x approaches negative 3 plus=

Answer 1

The Answers are:

1) Negative Infinity

2) Infinity

3) Negative Infinity

4) Infinity

Explanation:

I got them right!

Answer 2

`\displaystyle \lim_(x \to 3^-) f(x) = - \infty`

`\displaystyle \lim_(x \to 3^+) f(x) = \infty`

`\displaystyle \lim_(x \to -3^-) f(x) = - \infty`

`\displaystyle \lim_(x \to -3^+) f(x) = \infty`

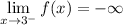
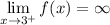
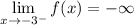
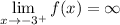
General Formulas and Concepts:

Algebra I

• Functions

Algebra II

• Analyzing Cartesian Planes and Graphs

Calculus

Limits

• Left Limit:
  `\displaystyle \lim_(x \to a^-) f(x)`
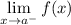
• Right Limit:
  `\displaystyle \lim_(x \to a^+) f(x)`

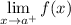
Graphical Limits

Explanation:

We approach this question by analyzing the graph. We notice we have asymptotes at x = -3 and x = 3.

Question 1

`\displaystyle \lim_(x \to 3^-) f(x) = \ ?`

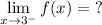
Essentially, the question is asking what the value is for f(x) when x approaches 3 from the left. We see from the graph f(x) that if we approach 3 from the left, we would be going towards the x = 3 asymptote, specifically -∞.

∴
`\displaystyle \lim_(x \to 3^-) f(x) = - \infty`

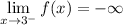
Question 2

`\displaystyle \lim_(x \to 3^+) f(x) = \ ?`

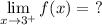
Essentially, the question is asking what the value is for f(x) when x approaches 3 from the right. We see from the graph f(x) that if we approach 3 from the right, we would be going towards the x = 3 asymptote, specifically ∞.

∴
`\displaystyle \lim_(x \to 3^+) f(x) = \infty`

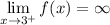
Question 3

`\displaystyle \lim_(x \to -3^-) f(x) = \ ?`

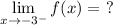
Essentially, the question is asking what the value is for f(x) when x approaches -3 from the left. We see from the graph f(x) that if we approach -3 from the left, we would be going towards the x = -3 asymptote, specifically -∞.

∴
`\displaystyle \lim_(x \to -3^-) f(x) = - \infty`

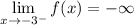
Question 4

`\displaystyle \lim_(x \to -3^+) f(x) = \ ?`

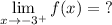
Essentially, the question is asking what the value is for f(x) when x approaches -3 from the right. We see from the graph f(x) that if we approach -3 from the right, we would be going towards the x = -3 asymptote, specifically ∞.

∴
`\displaystyle \lim_(x \to -3^+) f(x) = \infty`

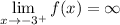
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Limits

Book: College Calculus 10e