Question

The Gonzales family has three children. On summer break, they went to an amusement park. They bought 3 child tickets for $18.50 and 2 adult tickets. If they spent a total of $104.50, how much was the price of EACH adult ticket?

Remember money is rounded to the nearest hundredth.

Answer 1

Your answer will be $
`$24.50`

Explanation:

Since for
`3` children tickets cost $
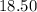`18.50` we will have to multiply $
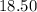`18.50` by 3.

`3` x $
`18.50` = $
`55.50`

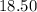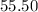
Now that we completed this step let's continue to the next part.

Since, we don't know the price of the adult tickets will will call it
`x` for now.

This time we will be using
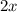`2x` to solve this equation.

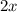`2x` refers to x is "twice a number"

$
`55.50+2x=` $
`104.50`

Now we should subtract $
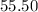`55.50` on both of the sides.

We will result in getting
`2x=49.`

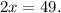
Our next step will be to divide
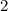`2` on both of the sides.

We will result in getting
`x=` $
`$24.50`

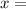Therefore, the price of the adult tickets is $24.50 each.

Answer 2

$24.50

Explanation:

Since we know that 3 child tickets are $18.50 each, let's find out the total price of the child tickets.

18.50 x 3 = $55.50

Since we don't know the cost of each of the adult tickets, let's call it x.

Now let's make an equation!

55.50 + 2x = 104.50

Now we have to isolate x in order to find out the price of each adult ticket.

Let's subtract 55.50 on both sides

2x = 49

Now let's divide 2 on both sides.

x = $24.50

So the price of an adult ticket is $24.50

CHECK:

55.50 times 2 (24.50) = 104.50