Answer:
Your answer will be $
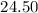
Explanation:
Since for
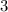 children tickets cost $
children tickets cost $
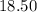 we will have to multiply $
we will have to multiply $
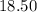 by 3.
by 3.
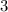 x $
x $
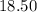 = $
= $
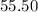
Now that we completed this step let's continue to the next part.
Since, we don't know the price of the adult tickets will will call it
 for now.
for now.
This time we will be using
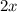 to solve this equation.
to solve this equation.
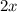 refers to x is "twice a number"
refers to x is "twice a number"
$
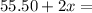 $
$
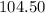
Now we should subtract $
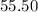 on both of the sides.
on both of the sides.
We will result in getting
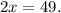
Our next step will be to divide
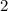 on both of the sides.
on both of the sides.
We will result in getting
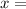 $
$
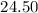
Therefore, the price of the adult tickets is $24.50 each.