Answer:
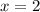
Explanation:
Given :-
And we need to find out the value of x. Well there is no specific method to solve the equation .This can be only done using the " Trial and error" Method.
- We know that , 3 , 4 and 5 are Pythagorean triplets . So the sum of squares of two smallest numbers is equal to the square of the largest number . Henceforth ,

Verification :-

So , the value of x is 2 . We can here prove that , x does not have other roots other than 2 . For that , divide the both sides of equation by
 , we have ,
, we have ,
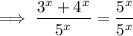
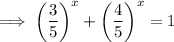
- Now if we take the value of x greater than 2 or less than 2 , then the value 1 will not be satisfied for the values of x greater than or less than 2 .
That is ,
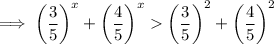
Subsequently :-
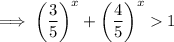
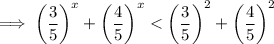
Subsequently :-
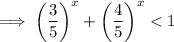
- Thus there is no other value other than 2 for which the value of above expression becomes 1 .
Hence 2 is the root of the given equation.