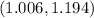Answer:
Hence, the mean of the potato chips lie between the interval
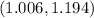
Given :
data is :
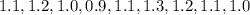
Confidence level is
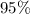 .
.
To find :
Confidence interval.
Explanation :
Mean
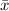
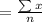
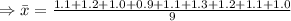
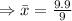
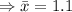
Standard deviation

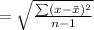
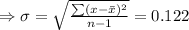
here,
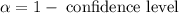
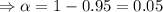
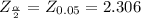 by the Z- table
by the Z- table
 confidence interval is :
confidence interval is :
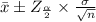
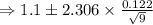
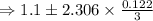
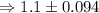
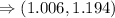
Therefore, the mean of the potato chips lie between the interval