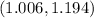Question

You are the product manager for Joe Totter Supermarket. You are interested in validating the contents of the one-pound bags of Keen potato chips. You select a random sample of 9 bags and empty the contents of each bag, one at a time, onto a scale and record the weights in pounds. Below are the recorded sample weights:

1.11.21.00.91.11.31.21.1

Assuming the weights of potato chips are normally distributed, estimate the mean weight of a bag of Keen potato chips using a 95% confidence interval.

Answer 1

Hence, the mean of the potato chips lie between the interval
`(1.006, 1.194)`

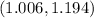
Given :

data is :

`1.1,1.2,1.0,0.9,1.1,1.3,1.2,1.1,1.0`

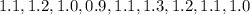
Confidence level is
`95\%`.

To find :

Confidence interval.

Explanation :

Mean
`\bar{x}`
`=(\sum x)/(n)`

`\Rightarrow \bar{x}=(1.1+1.2+1.0+0.9+1.1+1.3+1.2+1.1+1.0)/(9)`

`\Rightarrow \bar{x}=(9.9)/(9)`

`\Rightarrow \bar{x}=1.1`

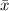
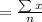
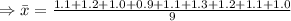
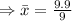
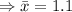
Standard deviation
`\sigma`
`=\sqrt{\frac{\sum (x-\bar{x})^2}{n-1}}`

`\Rightarrow \sigma=\sqrt{\frac{\sum (x-\bar{x})^2}{n-1}}=0.122`

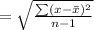
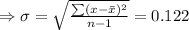
here,
`\alpha=1-\;\text{confidence level}`

`\Rightarrow \alpha=1-0.95=0.05`

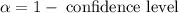
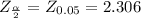`Z_{(\alpha)/(2)}=Z_(0.05)=2.306` by the Z- table

`95\%` confidence interval is :

`\bar{x}\pm Z_{(\alpha)/(2)}* (\sigma)/(√(n))`

`\Rightarrow 1.1\pm 2.306* (0.122)/(√(9))`

`\Rightarrow 1.1\pm 2.306* (0.122)/(3)`

`\Rightarrow 1.1\pm 0.094`

`\Rightarrow (1.006, 1.194)`

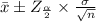
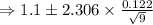
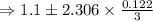
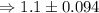
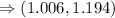
Therefore, the mean of the potato chips lie between the interval
`(1.006, 1.194)`