Question

A cone and a sphere both have a radius of 1. If you fill the cone with liquid, and pour it into the sphere, it fits exactly. What is the height of the cone? Show work

Answer 1

Answer and Step-by-step explanation:

First, solve for the volume of the sphere, then solve for the height of the cone using the volume of the sphere (which is said to be equal to the volume of the cone) and the radius given.

Volume formula of Sphere

V =
`(4)/(3) \pi r^2`

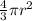
Substitute 1 in for r

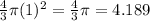`(4)/(3) \pi (1)^2 = (4)/(3) \pi = 4.189` = Volume

Finding the Height of a Cone

Volume formula for Cone:
`V = \pi r^2(h)/(3)`

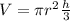
Solve for h

Multiply both sides by 3, then divide by pi and r^2.

`h = (3V)/(\pi r^2)`

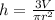
Plug in the volume and the radius.

`h = (3(4.189))/(\pi (1)^2)`

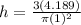
Simplify

`h = (12.567)/(\pi )`

h ≈ 4

4 is approximately the height.

#TeamTrees #PAW (Plant And Water)