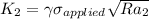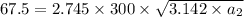Question

A structural component is fabricated from an alloy that has a plane strain fracture toughness of 45 MPam. It has been determined that this component fails at a stress of 300 MPa when the maximum length of a surface crack is 0.95 mm. What is the maximum allowable surface crack length (in mm) without fracture for this same component exposed to a stress of 300 MPa and made from another alloy with a plane strain fracture toughness of 67.5 MPam

Answer 1

Step-by-step explanation:

From the given information:

The first thing we need to do is to use the formula used in-plane strain fracture toughness to determine the geometry factor
`\gamma`

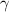
i.e

`K_1 = \gamma \sigma_(applied) √(Ra_1)`

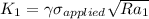
where;

a = crack length

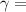`\gamma =` geometry factor

In the first scenario, where;

Plain fracture toughness
`K_1 = 45 \ MPa √(m)`

`\sigma _(applied) = 300 \ MPa \\ \\ a_1 = 6.95 * 10^(-3) m`

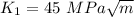
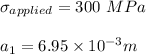
radius(R) = 3.142

Then, replacing it into the above equation, we have:

`45 MPa = \gamma (300 \ MPa ) \sqrt{3.142 * 0.95 * 10^(-3)} \\ \\ 45 \ MPa = 16.3902715 \gamma \\ \\ \gamma = (45 \ MPa)/(16.3902715) \\ \\ \gamma \ (geometry factor)= 2.745`

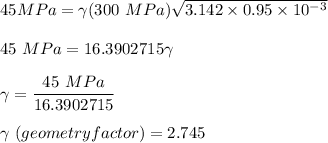
Now, since we've determined the geometry factor, it will be easier to estimate the max. allowable surface length.

∴

`K_2 = \gamma \sigma_(applied) √(Ra _2)`

`67.5= 2.745 * 300 * √(3.142 * a _2)`

`67.5= 1459.710372 √( a _2) \\ \\ (67.5)/( 1459.710372)= √( a _2) \\ \\ 0.0462420 = √( a _2) \\\\ a_2 = 0.0462420^2 \\ \\ a _ 2 = 0.002138 \\ \\ a_2 = 2.138* 10^(-3) \ m \\ \\ \mathbf{a_2 = 2.138\ mm}`