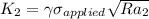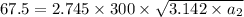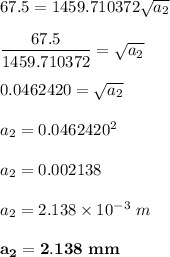Answer:
Step-by-step explanation:
From the given information:
The first thing we need to do is to use the formula used in-plane strain fracture toughness to determine the geometry factor
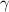
i.e

where;
a = crack length
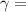 geometry factor
geometry factor
In the first scenario, where;
Plain fracture toughness
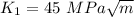
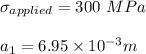
radius(R) = 3.142
Then, replacing it into the above equation, we have:
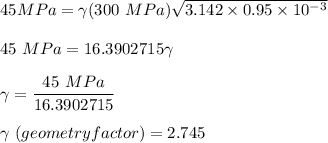
Now, since we've determined the geometry factor, it will be easier to estimate the max. allowable surface length.
∴