Question

Given f(x) =

2 cos(7x), for x < -1
2
for x > -1
COS (1x)
What is lim f(x)?
X - - 1

Answer 1

AAAAAAAAAAAAAAAAA

Step-by-step explanation: EDGE 2022

Answer 2

A

Explanation:

We are given the function:

`\displaystyle f(x) = \left\{ \begin{array}{ll} 2\cos(\pi x) \text{ for } x \leq -1 \\ \\ \displaystyle (2)/(\cos(\pi x))\text{ for } x > -1 \end{array} \right.`

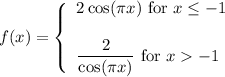
And we want to find:

`\displaystyle \lim_(x\to -1)f(x)`

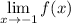
So, we need to determine whether or not the limit exists. In other words, we will find the two one-sided limits.

Left-Hand Limit:

`\displaystyle \lim_(x\to-1^-)f(x)`

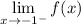
Since we are approaching from the left, we will use the first equation:

`\displaystyle =\lim_(x\to -1^-)2\cos(\pi x)`

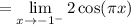
By direct substitution:

`=2\cos(\pi (-1))=2\cos(-\pi)=2(-1)=-2`

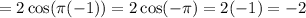
Right-Hand Limit:

`\displaystyle \lim_(x\to -1^+)f(x)`

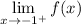
Since we are approaching from the right, we will use the second equation:

`=\displaystyle \lim_(x\to -1^+)(2)/(\cos(\pi x))`

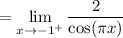
Direct substitution:

`\displaystyle =(2)/(\cos(\pi (-1)))=(2)/(\cos(-\pi))=(2)/((-1))=-2`

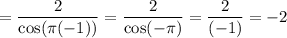
So, we can see that:

`\displaystyle \displaystyle \lim_(x\to-1^-)f(x)=\displaystyle \lim_(x\to -1^+)f(x) =-2`

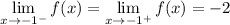
Since both the left- and right-hand limits exist and equal the same thing, we can conclude that:

`\displaystyle \lim_(x \to -1)f(x)=-2`

Our answer is A.