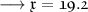Answer:
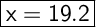
Explanation:
Here a right angled triangle is given to us and we need to find out the value of x . The measure of one of the sides is 24 and one of the acute angle is 53° .
- Here 24 is hypotenuse of the triangle and x is the perpendicular .
So here we may use the ratio of sine as ,
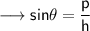
• On substituting the respective values ,

Substitute the value of sin 53° = 4/5 ,
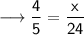
Cross multiply ,
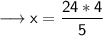
Simplify,