Question

Consider the following series.

1/4 + 1/8 + 1+12 + 1/16 + 1/20.....

Required:
Determine whether the geometric series is convergent or divergent.

Answer 1

The series is convergent.

Explanation:

1/4 + 1/8 + 1+12 + 1/16 + 1/20

In each term, the numerator stays 1, while the denominator is multiplied by 4. Thus, the series is given by:

`\sum_(n=1)^(\infty) (1)/(4n)`

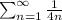
Convergence test:

We compare the sequence of this test,
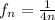`f_n = (1)/(4n)`, with a sequence
`g_n = (1)/(n)`.

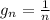If
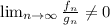`\lim_(n \rightarrow \infty) (f_n)/(g_n) \\eq 0`, the series is convergent. So

`\lim_(n \rightarrow \infty) (f_n)/(g_n) = \lim_(n \rightarrow \infty) ((1)/(4n))/((1)/(n)) =  \lim_(n \rightarrow \infty) (n)/(4n) = \lim_(n \rightarrow \infty) (1)/(4) = (1)/(4) \\eq 0`

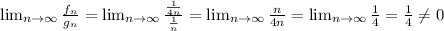
As the limit is different of zero, the series is convergent.