Question

A survey of 300 students from a New York State School District reveals that 112 favor year round school with two week vacations every ten weeks. Construct the 98% confidence interval for the true population proportion of all New York students who favor year round school.

Answer 1

The 98% confidence interval for the true population proportion of all New York students who favor year round school is (0.3083, 0.4383).

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

A survey of 300 students from a New York State School District reveals that 112 favor year round school with two week vacations every ten weeks.

This means that
`n = 300, \pi = (112)/(300) = 0.3733`

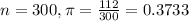
98% confidence level

So
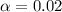`\alpha = 0.02`, z is the value of Z that has a p-value of
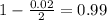`1 - (0.02)/(2) = 0.99`, so
`Z = 2.327`.

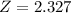The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.3733 - 2.327\sqrt{(0.3733*0.6267)/(300)} = 0.3083`

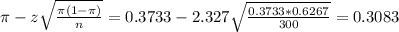
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.3733 + 2.327\sqrt{(0.3733*0.6267)/(300)} = 0.4383`

The 98% confidence interval for the true population proportion of all New York students who favor year round school is (0.3083, 0.4383).