Answer:
Assuming that you actually mean that if
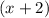 is a factor of
is a factor of
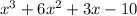 , the answer is yes.
, the answer is yes.
Explanation:
We need to do long division of the polynomial to figure out if this is true. I would show it here, but it is extremely difficult to do so. (Maybe someone could help me.) When I factor it, it does not leave a remainder, so this is true.
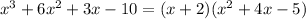
Another way one could figure this out is by graphing the equation
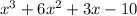 on your graphing calculator or on just a graphing website, lake Desmos. The screenshot below shows the graph.
on your graphing calculator or on just a graphing website, lake Desmos. The screenshot below shows the graph.
The polynomial will have a factor of
 if the point
if the point
 exists on the graph. The graph has the following three zeroes.
exists on the graph. The graph has the following three zeroes.
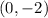 ,
,
 , and
, and
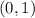
As such, it has the three factors
 ,
,
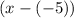 , and
, and
 .
.
Since
 , it is a factor of the polynomial.
, it is a factor of the polynomial.