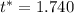Answer:
Step-by-step explanation:
Given
 --- sample
--- sample
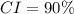 --- confidence interval
--- confidence interval
Required
Determine the critical value
Start by calculating the degrees of freedom (df)
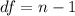
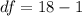
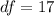
Next, calculate the significance level
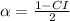
This gives:
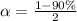
Express percentage as decimal
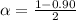
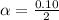
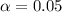
Next, we look at the t table at
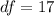
and
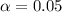
We have the critical value to be: