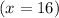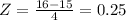Answer:
Hence, the score for each of the five observations are
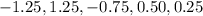
Given :
Sample with data values of
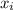
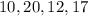 and
and
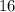
Sample size
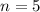
To find:
Compute the score for each of the five observations.
Explanation :
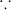 Sample mean
Sample mean
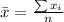
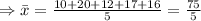
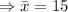
Standard deviation
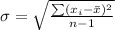
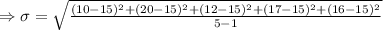
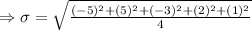
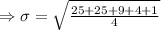
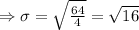
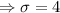
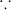 The score of the observations
The score of the observations
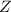 is
is
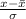 .
.
So, when
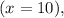
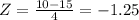
when
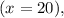
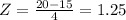
when
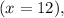
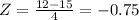
when
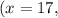
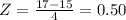
when