Question

Steam enters a turbine with a pressure of 30 bar, a temperature of 400 oC, and a velocity of 160 m/s. Saturated vapor at 100 oC exits with a velocity of 100 m/s. At steady state, the turbine develops work equal to 540 kJ per kg of steam flowing through the turbine. Heat transfer between the turbine and its surroundings occurs at an average outer surface temperature of 350 K. Determine the rate at which entropy is produced within the turbine per kg of steam flo

Answer 1

The rate at which entropy is produced within the turbine is 22.762 kilojoules per kilogram-Kelvin.

Step-by-step explanation:

By either the Principle of Mass Conservation and First and Second Laws of Thermodynamics, we model the steam turbine by the two equations described below:

Principle of Mass Conservation

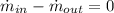`\dot m_(in) - \dot m_(out) = 0` (1)

First Law of Thermodynamics

`-\dot Q_(out) + \dot m \cdot \left[h_(in)-h_(out)+ (1)/(2)\cdot (v_(in)^(2)-v_(out)^(2)) - w_(out) \right] = 0` (2)

Second Law of Thermodynamics

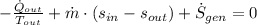`-(\dot Q_(out))/(T_(out)) + \dot m\cdot (s_(in)-s_(out)) + \dot S_(gen) = 0` (3)

By dividing each each expression by
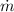`\dot m`, we have the following system of equations:

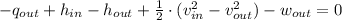`-q_(out) + h_(in)-h_(out) + (1)/(2)\cdot (v_(in)^(2)-v_(out)^(2)) - w_(out) = 0` (2b)

`-(q_(out))/(T_(out)) + s_(in)-s_(out) + s_(gen) = 0` (3b)

Where:

`\dot Q_(out)` - Heat transfer rate between the turbine and its surroundings, in kilowatts.

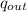`q_(out)` - Specific heat transfer between the turbine and its surroundings, in kilojoules per kilogram.

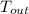`T_(out)` - Outer surface temperature of the turbine, in Kelvin.

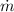`\dot m` - Mass flow rate through the turbine, in kilograms per second.

`h_(in)`,
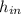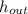`h_(out)` - Specific enthalpy of water at inlet and outlet, in kilojoules per kilogram.

`v_(in)`,
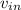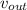`v_(out)` - Speed of water at inlet and outlet, in meters per second.

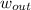`w_(out)` - Specific work of the turbine, in kilojoules per kilogram.

`s_(in)`,
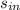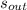`s_(out)` - Specific entropy of water at inlet and outlet, in kilojoules per kilogram-Kelvin.

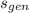`s_(gen)` - Specific generated entropy, in kilojoules per kilogram-Kelvin.

By property charts for steam, we get the following information:

Inlet

`T = 400\,^(\circ)C`,
`p = 3000\,kPa`,
`h = 3231.7\,(kJ)/(kg)`,
`s = 6.9235\,(kJ)/(kg\cdot K)`

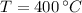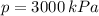Outlet

`T = 100\,^(\circ)C`,
`p = 101.42\,kPa`,
`h = 2675.6\,(kJ)/(kg)`,
`s = 7.3542\,(kJ)/(kg\cdot K)`

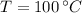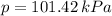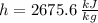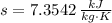
If we know that
`h_(in) = 3231.7\,(kJ)/(kg)`,
`h_(out) = 2675.6\,(kJ)/(kg)`,
`v_(in) = 160\,(m)/(s)`,
`v_(out) = 100\,(m)/(s)`,
`w_(out) = 540\,(kJ)/(kg)`,
`T_(out) = 350\,K`,
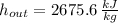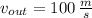`s_(in) = 6.9235\,(kJ)/(kg\cdot K)` and
`s_(out) = 7.3542\,(kJ)/(kg\cdot K)`, then the rate at which entropy is produced withing the turbine is:

`q_(out) = h_(in) - h_(out) + (1)/(2)\cdot (v_(in)^(2)-v_(out)^(2))-w_(out)`

`q_(out) = 3231.7\,(kJ)/(kg) - 2675.6\,(kJ)/(kg) + (1)/(2)\cdot \left[\left(160\,(m)/(s) \right)^(2)-\left(100\,(m)/(s) \right)^(2)\right] - 540\,(kJ)/(kg)`

`q_(out) = 7816.1\,(kJ)/(kg)`

`s_(gen) = (q_(out))/(T_(out))+s_(out)-s_(in)`

`s_(gen) = (7816.1\,(kJ)/(kg) )/(350\,K) + 7.3542\,(kJ)/(kg\cdot K) - 6.9235\,(kJ)/(kg\cdot K)`

`s_(gen) = 22.762\,(kJ)/(kg\cdot K)`

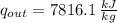
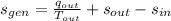
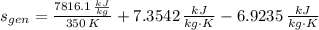
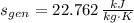
The rate at which entropy is produced within the turbine is 22.762 kilojoules per kilogram-Kelvin.