Answer:
The rate at which entropy is produced within the turbine is 22.762 kilojoules per kilogram-Kelvin.
Step-by-step explanation:
By either the Principle of Mass Conservation and First and Second Laws of Thermodynamics, we model the steam turbine by the two equations described below:
Principle of Mass Conservation
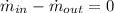 (1)
(1)
First Law of Thermodynamics
![-\dot Q_(out) + \dot m \cdot \left[h_(in)-h_(out)+ (1)/(2)\cdot (v_(in)^(2)-v_(out)^(2)) - w_(out) \right] = 0](https://img.qammunity.org/2022/formulas/engineering/college/wlwgbyhkg0u7nittuduba0bvy0j9nqskt1.png) (2)
(2)
Second Law of Thermodynamics
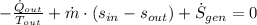 (3)
(3)
By dividing each each expression by
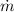 , we have the following system of equations:
, we have the following system of equations:
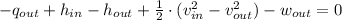 (2b)
(2b)
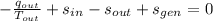 (3b)
(3b)
Where:
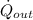 - Heat transfer rate between the turbine and its surroundings, in kilowatts.
- Heat transfer rate between the turbine and its surroundings, in kilowatts.
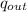 - Specific heat transfer between the turbine and its surroundings, in kilojoules per kilogram.
- Specific heat transfer between the turbine and its surroundings, in kilojoules per kilogram.
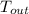 - Outer surface temperature of the turbine, in Kelvin.
- Outer surface temperature of the turbine, in Kelvin.
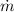 - Mass flow rate through the turbine, in kilograms per second.
- Mass flow rate through the turbine, in kilograms per second.
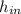 ,
,
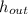 - Specific enthalpy of water at inlet and outlet, in kilojoules per kilogram.
- Specific enthalpy of water at inlet and outlet, in kilojoules per kilogram.
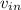 ,
,
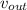 - Speed of water at inlet and outlet, in meters per second.
- Speed of water at inlet and outlet, in meters per second.
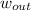 - Specific work of the turbine, in kilojoules per kilogram.
- Specific work of the turbine, in kilojoules per kilogram.
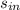 ,
,
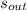 - Specific entropy of water at inlet and outlet, in kilojoules per kilogram-Kelvin.
- Specific entropy of water at inlet and outlet, in kilojoules per kilogram-Kelvin.
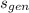 - Specific generated entropy, in kilojoules per kilogram-Kelvin.
- Specific generated entropy, in kilojoules per kilogram-Kelvin.
By property charts for steam, we get the following information:
Inlet
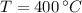 ,
,
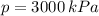 ,
,
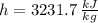 ,
,
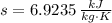
Outlet
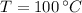 ,
,
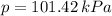 ,
,
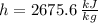 ,
,
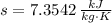
If we know that
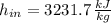 ,
,
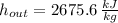 ,
,
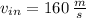 ,
,
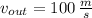 ,
,
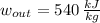 ,
,
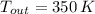 ,
,
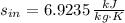 and
and
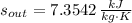 , then the rate at which entropy is produced withing the turbine is:
, then the rate at which entropy is produced withing the turbine is:
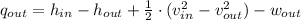
![q_(out) = 3231.7\,(kJ)/(kg) - 2675.6\,(kJ)/(kg) + (1)/(2)\cdot \left[\left(160\,(m)/(s) \right)^(2)-\left(100\,(m)/(s) \right)^(2)\right] - 540\,(kJ)/(kg)](https://img.qammunity.org/2022/formulas/engineering/college/59392s7m3xtjfnriu25pdwrgm0mqkrko30.png)
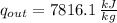
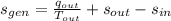
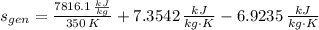
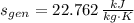
The rate at which entropy is produced within the turbine is 22.762 kilojoules per kilogram-Kelvin.