Answer:
81.74% probability that the sum of the 95 wait times you observed is between 670 and 796
Explanation:
To solve this question, the uniform probability distribution and the normal probability distribution must be understood.
Uniform distribution:
A distribution is called uniform if each outcome has the same probability of happening.
The distribution has two bounds, a and b.
Its mean is given by:
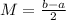
Its standard deviation is given by:
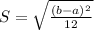
Normal distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
n instances of the uniform distribution can be approximated to the normal with
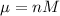 ,
,

Uniformly distributed over the interval [0,15].
This means that:
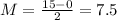
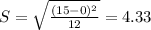
95 trains
 , so:
, so:
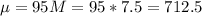
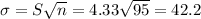
What is the approximate probability (to 2 decimal places) that the sum of the 95 wait times you observed is between 670 and 796?
This is the pvalue of Z when X = 796 subtracted by the pvalue of Z when X = 670. So
X = 796


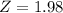
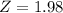 has a pvalue of 0.9761
has a pvalue of 0.9761
X = 670

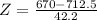
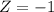
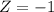 has a pvalue of 0.1587
has a pvalue of 0.1587
0.9761 - 0.1587 = 0.8174
81.74% probability that the sum of the 95 wait times you observed is between 670 and 796