Question

A machine produces 3-inch nails. A sample of 10 nails is obtained and the lengths determined. After some calculation, the sample mean is 2.98 and the sample standard deviation is 0.09. Find a 90% confidence interval for the population mean length of nails produce by the machine. Please input the upper limit of the confidence interval

Answer 1

The 90% confidence interval for the population mean length of nails produced by the machine.

(2.91562, 3.04438)

Explanation:

Step:1

Given that the size of the sample 'n' = 10

Given that the mean of the sample (x⁻) = 2.98

Given that the standard deviation of the sample (s) = 0.09

Degrees of freedom = n-1 = 10 -1 = 9

t₀.₁₀ = 2.2621

Step:2

The 90% confidence interval for the population mean length of nails produced by the machine.

`(x^(-) - t_(9 , 0.10) (S)/(√(n) ) , x^(-) + t_(9,0.10) (S)/(√(n) ) )`

`(2.98 - 2.2621((0.09)/(√(10) ) , 2.98 + 2.262 (0.09)/(√(10) ) )`

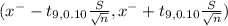
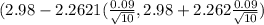
(2.98 - 0.06438 , 2.98 + 0.06438)

(2.91562 , 3.04438)

Final answer:-

The 90% confidence interval for the population mean length of nails produced by the machine.

(2.91562, 3.04438)