Answer:
The 90% confidence interval for the population mean length of nails produced by the machine.
(2.91562, 3.04438)
Explanation:
Step:1
Given that the size of the sample 'n' = 10
Given that the mean of the sample (x⁻) = 2.98
Given that the standard deviation of the sample (s) = 0.09
Degrees of freedom = n-1 = 10 -1 = 9
t₀.₁₀ = 2.2621
Step:2
The 90% confidence interval for the population mean length of nails produced by the machine.
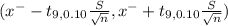

(2.98 - 0.06438 , 2.98 + 0.06438)
(2.91562 , 3.04438)
Final answer:-
The 90% confidence interval for the population mean length of nails produced by the machine.
(2.91562, 3.04438)