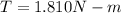Answer:

Step-by-step explanation:
From the question we are told that:
Radius
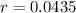
Number of turns
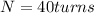
Current
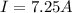
Magnetic Field
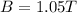
Generally the equation for magnetic moment M is mathematically given by

Where
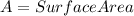
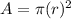
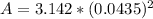
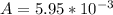
Therefore the magnetic moment is given as

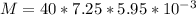

Generally the equation for Torque on the coil T is mathematically given by
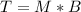
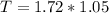
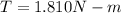
Therefore torque on coil T is given a