Question

A tank initially contains 100 gallons of brine with 10 lb of salt dissolved in it. Brinecontaining 0.4 lb of salt per gallon ows from an outside source into the tank at a rateof 5 gal/min. The mixture is discharged out of the tank at the same rate of 5 gal/min..Assume that solutions are well-stirred at all times.

Required:
Find the amount of salt in the tank at the end of 40 minutes.

Answer 1

35.94 lb

Explanation:

The net mass flow rate dm/dt = flow rate in - flow rate out

mass flow rate in = concentration in × volume flow rate in = 0.4 lb/gallon of salt × 5 gal/min = 2 lb/min

Let m(t) be the mass present at time, t.

So, the concentration at time, t = m(t)/volume of tank = m(t)/100

mass flow rate out = concentration out × volume flow rate out = m(t)/100 lb/gal× 5 gal/min = m(t)/20 lb/min

So, dm/dt = 2 lb/min - m(t)/20 lb/min

So, dm/dt = 2 - m(t)/20

dm/dt = [40 - m(t)]/20

separating the variables, we have

dm/[40 - m(t)] = dt/20

integrating, we have

∫dm/[40 - m(t)] = ∫dt/20

-1/-1 ×∫dm/[40 - m(t)] = ∫dt/20

1/-1 ×∫-dm/[40 - m(t)] = ∫dt/20

1/-1 ×㏑[40 - m(t)] = t/20 + C

-㏑[40 - m(t)] = t/20 + C

㏑[40 - m(t)] = -t/20 - C

taking exponents of both sides, we have

`40 - m(t) = e^({(-t)/(20) - C}) \\40 - m(t) = e^{(-t)/(20)}e^(-C) \\40 - m(t) = Ae^{(-t)/(20)} (A = e^(-C))\\m(t) = 40 - Ae^{(-t)/(20)}`

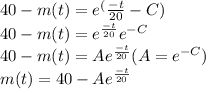
when t = 0 m(0) = 10 lb

So

`m(t) = 40 - Ae^{(-t)/(20)}\\m(0) = 40 - Ae^{(-0)/(20)}\\10 = 40 - Ae^(0)\\10 = 40 - A\\A = 40 - 10 \\A = 30`

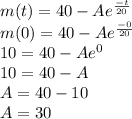
So,

`m(t) = 40 - 30e^{(-t)/(20)}`

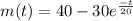
when t = 40 minutes, m(40) =

`m(40) = 40 - 30e^{(-40)/(20)}\\m(40) = 40 - 30e^(-2)\\m(40) = 40 - 30 X 0.1353\\m(40) = 40 - 4.06\\m(40) = 35.94`

So, at the end of 40 minutes, the amount of salt in the tank is 35.94 lb