Answer:
35.94 lb
Explanation:
The net mass flow rate dm/dt = flow rate in - flow rate out
mass flow rate in = concentration in × volume flow rate in = 0.4 lb/gallon of salt × 5 gal/min = 2 lb/min
Let m(t) be the mass present at time, t.
So, the concentration at time, t = m(t)/volume of tank = m(t)/100
mass flow rate out = concentration out × volume flow rate out = m(t)/100 lb/gal× 5 gal/min = m(t)/20 lb/min
So, dm/dt = 2 lb/min - m(t)/20 lb/min
So, dm/dt = 2 - m(t)/20
dm/dt = [40 - m(t)]/20
separating the variables, we have
dm/[40 - m(t)] = dt/20
integrating, we have
∫dm/[40 - m(t)] = ∫dt/20
-1/-1 ×∫dm/[40 - m(t)] = ∫dt/20
1/-1 ×∫-dm/[40 - m(t)] = ∫dt/20
1/-1 ×㏑[40 - m(t)] = t/20 + C
-㏑[40 - m(t)] = t/20 + C
㏑[40 - m(t)] = -t/20 - C
taking exponents of both sides, we have
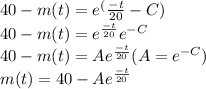
when t = 0 m(0) = 10 lb
So
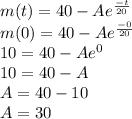
So,
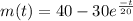
when t = 40 minutes, m(40) =
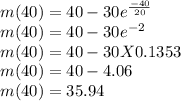
So, at the end of 40 minutes, the amount of salt in the tank is 35.94 lb