Question

Help, so You pick a card at random. Without putting the first card back, you pick a second card at random. There are 3 cards, a 5 a 6 and a 7 What is the probability of picking a 5 and then picking a 6?

Answer 1

Given:

There are 3 cards, a 5 a 6 and a 7.

You pick a card at random. Without putting the first card back, you pick a second card at random.

To find:

The probability of picking a 5 and then picking a 6.

Solution:

We have,

Total number of cards = 3

Number of card of 5 = 1

So, probability of getting a card of 5 is:

`P(5)=\frac{\text{Number of card of 5}}{\text{Total number of cards}}`

`P(5)=(1)/(3)`

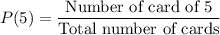
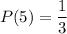
After this selection, the remaining number of cards is 2. So, probability of getting a card of 6 in second draw is:

`P(6)=\frac{\text{Number of card of 6}}{\text{Total number of remaining cards}}`

`P(6)=(1)/(2)`

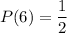
Now, the probability of picking a 5 and then picking a 6 is

`P(\text{5 then 6})=P(5)* P(6)`

`P(\text{5 then 6})=(1)/(3)* (1)/(2)`

`P(\text{5 then 6})=(1)/(6)`

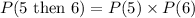
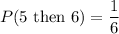
Therefore, the probability of picking a 5 and then picking a 6 is
`(1)/(6)`.