Question

An engineer designed a valve that will regulate water pressure on an automobile engine. The engineer designed the valve such that it would produce a mean pressure of 5.7 pounds/square inch. It is believed that the valve performs above the specifications. The valve was tested on 8 engines and the mean pressure was 6.2 pounds/square inch with a variance of 0.49. A level of significance of 0.05 will be used. Assume the population distribution is approximately normal. Make the decision to reject or fail to reject the null hypothesis.

Answer 1

The p-value of the test is 0.0416 < 0.05, which means that the null hypothesis is rejected.

Explanation:

The engineer designed the valve such that it would produce a mean pressure of 5.7 pounds/square inch. It is believed that the valve performs above the specifications.

At the null hypothesis, we test that the mean is the specification value of 5.7, that is:

`H_0: \mu = 5.7`

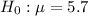
At the alternate hypothesis, we test that the mean is above the specifications, that is, above 5.7. So:

`H_a: \mu > 5.7`

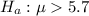
The test statistic is:

`t = (X - \mu)/((s)/(√(n)))`

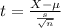
In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.

5.7 is tested at the null hypothesis:

This means that
`\mu = 5.7`

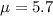
The valve was tested on 8 engines and the mean pressure was 6.2 pounds/square inch with a variance of 0.49.

This means that
`n = 8, X = 6.2, s = √(0.49) = 0.7`

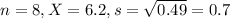
Test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (6.2 - 5.7)/((0.7)/(√(8)))`

`t = 2.02`

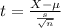
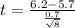
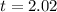
P-value of the test and decision:

The p-value of the test is the probability of finding a sample mean above 6.2, which is the p-value of t = 2.02, using a right-tailed test with 8 - 1 = 7 degrees of freedom.

With the help of a calculator, this p-value is 0.0416.

The p-value of the test is 0.0416 < 0.05, which means that the null hypothesis is rejected.