Answer:
The p-value of the test is 0.0416 < 0.05, which means that the null hypothesis is rejected.
Explanation:
The engineer designed the valve such that it would produce a mean pressure of 5.7 pounds/square inch. It is believed that the valve performs above the specifications.
At the null hypothesis, we test that the mean is the specification value of 5.7, that is:

At the alternate hypothesis, we test that the mean is above the specifications, that is, above 5.7. So:
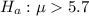
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.
is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.
5.7 is tested at the null hypothesis:
This means that

The valve was tested on 8 engines and the mean pressure was 6.2 pounds/square inch with a variance of 0.49.
This means that

Test statistic:

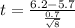
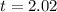
P-value of the test and decision:
The p-value of the test is the probability of finding a sample mean above 6.2, which is the p-value of t = 2.02, using a right-tailed test with 8 - 1 = 7 degrees of freedom.
With the help of a calculator, this p-value is 0.0416.
The p-value of the test is 0.0416 < 0.05, which means that the null hypothesis is rejected.