Question

A round asteroid has a surface gravity of .0288 m/s^2 if the mass of the asteroid is 1.10 x10^18 kg what is its radius

Answer 1

5.05x10^4

Step-by-step explanation:

g=(GM)/r^2, so

.0288=(6.67x10^-11*1.10x10^18)/r^2, r=5.05x10^4.

This is correct on Acellus.

Answer 2

r = 50.47 x 10³ m = 50.47 km

Step-by-step explanation:

Using the formula for the acceleration due to gravity:

`g = (Gm)/(r^2)`

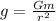
where,

g = acceleration due to gravity on the surface of asteroid = 0.0288 m/s²

G = Universal Gravitational Constant = 6.67 x 10⁻¹¹ Nm²/kg²

m= mass of asteroid = 1.1 x 10¹⁸ kg

r = radius of asteroid = ?

Therefore,

`0.0288\ m/s^2 = ((6.67\ x\ 10^(-11)\ Nm^2/kg^2)(1.1\ x\ 10^(18)\ kg))/(r^2) \\\\r = \sqrt{((6.67\ x\ 10^(-11)\ Nm^2/kg^2)(1.1\ x\ 10^(18)\ kg))/(0.0288\ m/s^2)}`

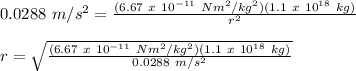
r = 50.47 x 10³ m = 50.47 km